ANAND CLASSES study material and notes to learn about the rolling motion of a wheel with a detailed explanation, velocity analysis, and NEET 2024 question. Understand the concepts of pure rolling, velocity of different points, and key takeaways for NEET Physics preparation.
📌 NEET 2024 Physics Question
Rolling Motion of a Wheel – NEET 2024 Question & Explanation
A wheel of a bullock cart is rolling on a level road as shown in the figure. If its linear speed is $v$ in the direction shown, which one of the following options is correct regarding points P and Q (highest and lowest points on the wheel, respectively)?
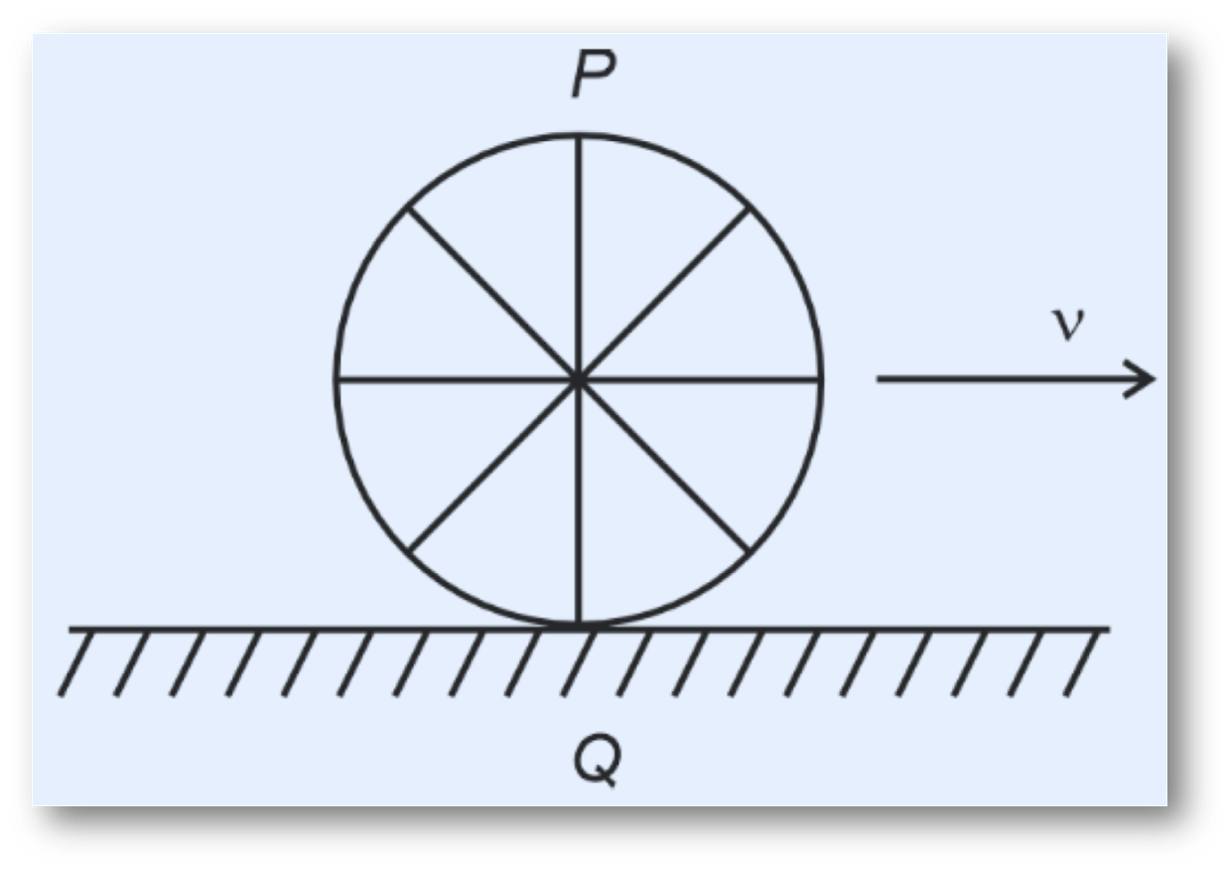
📝 Given Options:
- Point P moves slower than point Q
- Point P moves faster than point Q ✅
- Both points P and Q move with equal speed
- Point P has zero speed
📌 Related Posts:
NEET 2024 Physics PYQ Question-A logic circuit provides the output Y as per the truth table. The expression for the output Y is
📚 Concept Explanation: Pure Rolling Motion
In pure rolling, the wheel has two types of motion:
1️⃣ Translational Motion: The entire wheel moves forward with velocity $v$.
2️⃣ Rotational Motion: The wheel spins about its center with angular velocity $\omega$.
Since the wheel is rolling without slipping: $v = \omega r$
Each point on the wheel has a velocity due to both translation and rotation.
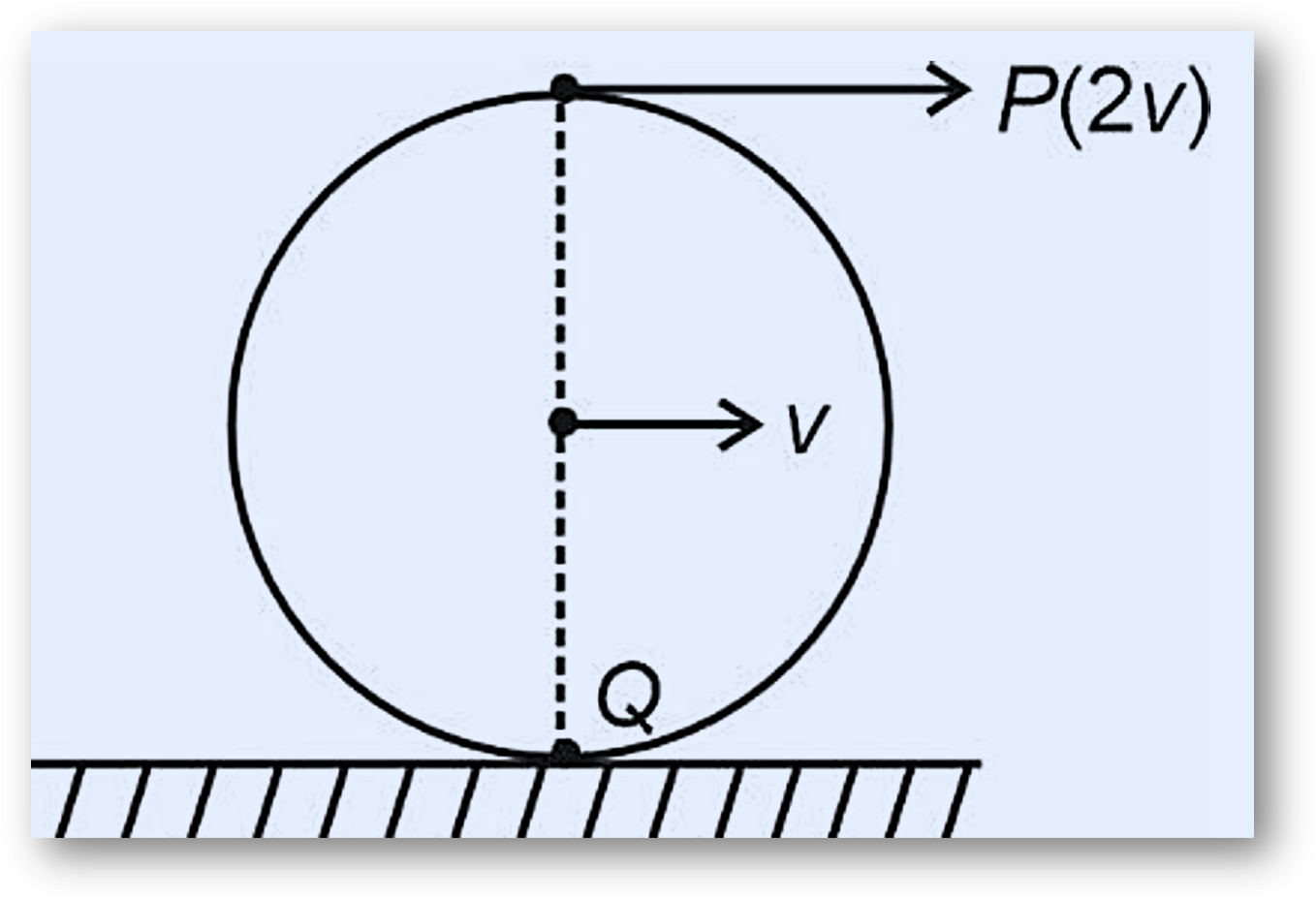
🔍 Velocity Analysis at Different Points
Let’s analyze the velocity at three key points:
1️⃣ Center of the Wheel (O)
- Translational velocity = $v$
- No rotational contribution at the center.
- Total velocity at the center: $v_O = v$
2️⃣ Topmost Point (P)
- Translational velocity = $v$ (same as the center, moving forward).
- Rotational velocity due to spinning: $v_r = \omega r = v$ (also forward).
- Total velocity at P: $v_P = v + v = 2v$
✅ The topmost point moves forward with twice the velocity of the center.
3️⃣ Bottommost Point (Q) (Point of Contact with Ground)
- Translational velocity = $v$ (same as the center, moving forward).
- Rotational velocity = $-v$ (opposite direction due to spinning).
- Total velocity at Q: $v_Q = v – v = 0$
🚨 The bottommost point has zero velocity relative to the ground. This is why the wheel rolls without slipping.
📊 Velocity Summary Table
| Point | Translational Velocity ($v$) | Rotational Velocity ($v_r$) | Total Velocity |
|---|---|---|---|
| Center (O) | $v$ | 0 | $v$ |
| Topmost Point (P) | $v$ | $v$ | $2v$ |
| Bottommost Point (Q) | $v$ | $-v$ | 0 |
✅ Answer Selection
Now, let’s check the options again:
- Point P moves slower than point Q ❌
- Incorrect, because $v_P = 2v$ and $v_Q = 0$, so P is actually faster.
- Point P moves faster than point Q ✅
- Correct! P moves with speed $2v$, while Q is stationary.
- Both points move with equal speed ❌
- Incorrect, since $v_P = 2v$ and $v_Q = 0$.
- Point PP has zero speed ❌
- Incorrect, P has the highest speed $2v$.
🎯 Correct Answer:
(2) Point P moves faster than point Q$\boxed{(2) \text{ Point } P \text{ moves faster than point } Q}$
🔎 Important Takeaways
✔️ In pure rolling, the bottommost point always has zero velocity.
✔️ The topmost point moves with the highest velocity, equal to$\:2v$.
✔️ This principle is crucial in understanding motion of bicycle wheels, car tires, and even planetary rotation!
📝 Do You Know?
🔹 If rolling is not pure (slipping occurs), the bottommost point will have a nonzero velocity, causing friction to act.
🔹 In high-speed cycling, the topmost part of the wheel moves much faster than the cycle itself!
🔹 This concept helps in designing efficient tires for vehicles, ensuring minimal slipping and maximum grip.
🧩 Practice Questions
💡 Question 1:
A bicycle wheel rolls on the ground with velocity $v$. What is the speed of a point halfway between the center and the top?
(A) $v$
(B) $1.5v$
(C) $2v$
(D) $0.5v$
💡 Question 2:
A rolling disc has an angular velocity of $10 \text{ rad/s}$ and a radius of 0.50.5 m. What is the velocity of the topmost point?
(A) $5 \text{ m/s}$
(B) $10 \text{ m/s}$
(C) $15 \text{ m/s}$
(D) $20 \text{ m/s}$
📚 NEET 2024 Study Material?
✅ Anand Classes provides expert coaching for NEET, JEE, and CBSE Board exams.
📖 Get detailed notes, test papers, and mock exams to boost your preparation!
📞 Contact us: +91-9463138669



