ANAND CLASSES Study Material and Notes to learn the geometric derivation of trigonometric ratios for 30°, 45°, and 60° with diagrams, formulas, and step-by-step explanations. Ideal for Class 10, Class 11, JEE, and NEET preparation.
📌 Related Posts:
Trigonometry Class 10 Solved Problems and Examples, Prove Identities by Given Angle
|
Trigonometric Ratios | Definitions, Formulas & Identities, Solved Examples
|
Trigonometric Identities Class 10 – Solved Problems & Examples
|
Trigonometry JEE Foundation Important Solved Problems and Examples
|
Trigonometric Ratios NTSE JEE Foundation Important Solved Examples and Problems
📚 Trigonometric Ratios of 45°, 60°, and 30° (Geometrically Explained) for Class 10 Math
Trigonometric ratios are the relationships between the sides of a right-angled triangle and its angles. Let’s derive the exact values of trigonometric ratios for 45°, 60°, and 30° using basic geometry and Pythagoras’ Theorem.
🔺 TRIGONOMETRIC RATIOS OF 45° for Class 10 Math
🔧 Construction:
Take a right-angled triangle ΔABC with:
- ∠B = 90°
- ∠A = ∠C = 45° (Since the sum of angles in triangle is 180°)
As ∠A = ∠C, the triangle is isosceles with:
- AB = BC = a units (equal sides)
- AC = hypotenuse
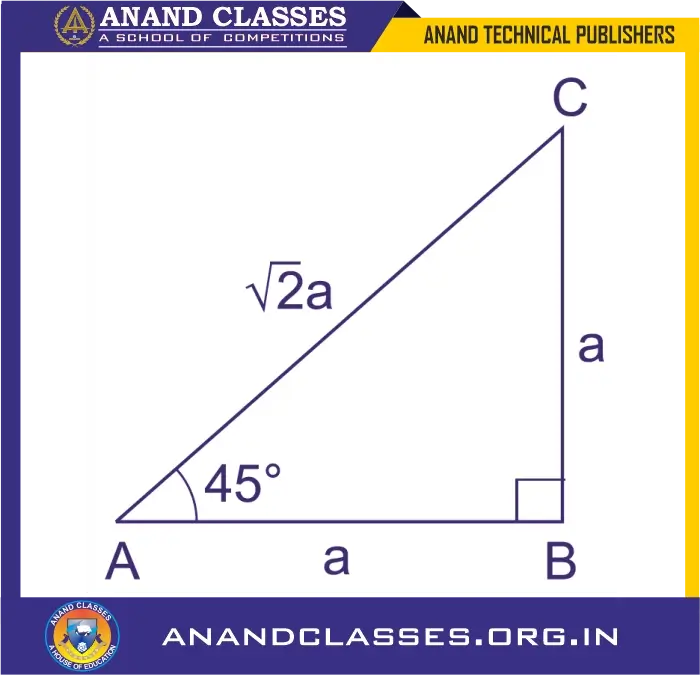
Using Pythagoras’ Theorem:
$$AC = \sqrt{AB^2 + BC^2} = \sqrt{a^2 + a^2} = \sqrt{2a^2} = a\sqrt{2}$$
🧮 T-Ratios of 45°:
$$\sin 45^\circ = \frac{BC}{AC} = \frac{a}{a\sqrt{2}} = \frac{1}{\sqrt{2}} $$
$$\cos 45^\circ = \frac{AB}{AC} = \frac{a}{a\sqrt{2}} = \frac{1}{\sqrt{2}}$$
$$\tan 45^\circ = \frac{BC}{AB} = \frac{a}{a} = 1 $$
$$\sec 45^\circ = \frac{1}{\cos 45^\circ} = \sqrt{2} $$
$$\mathrm{cosec} \:45^\circ = \frac{1}{\sin 45^\circ} = \sqrt{2} $$
$$\cot 45^\circ = \frac{1}{\tan 45^\circ} = 1$$
🔺 TRIGONOMETRIC RATIOS OF 60° AND 30° for Class 10 Math
🔧 Construction:
Consider an equilateral triangle ΔABC:
- Each side = 2a
- Each angle = 60°
Draw a perpendicular AD from vertex A to base BC.
Then:
- AD ⊥ BC
- BD = DC = a (since it bisects BC)
- ∠ADB = 90°
- ∠BAD = 30°, ∠DAC = 30°, ∠ADB = 90°, ∠DAB = 60°
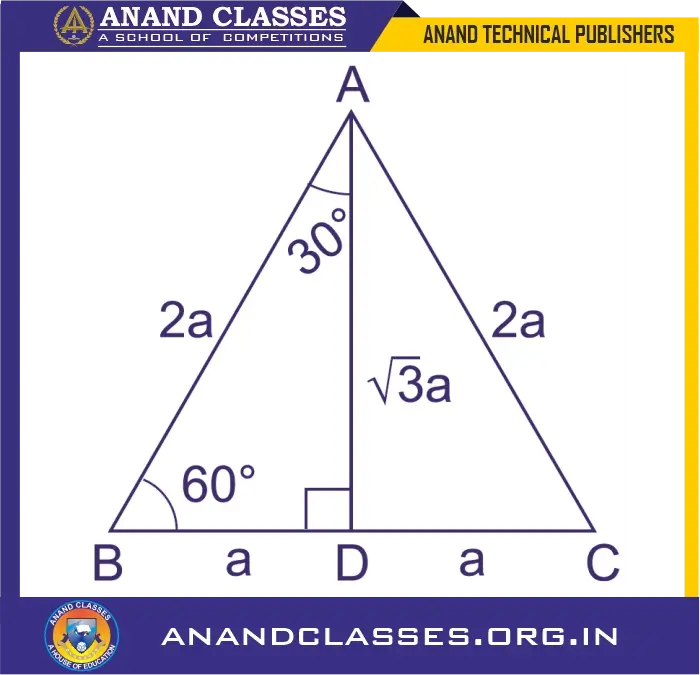
Using Pythagoras in ΔADB:
$$AD = \sqrt{AB^2 – BD^2} = \sqrt{(2a)^2 – a^2} = \sqrt{4a^2 – a^2} = \sqrt{3a^2} = a\sqrt{3}$$
✅ T-Ratios of 60° (from ΔADB):
- Base = BD = a
- Height = AD = $a\sqrt{3}$
- Hypotenuse = AB = 2a
$$\sin 60^\circ = \frac{AD}{AB} = \frac{a\sqrt{3}}{2a} = \frac{\sqrt{3}}{2} $$
$$\cos 60^\circ = \frac{BD}{AB} = \frac{a}{2a} = \frac{1}{2} $$
$$\tan 60^\circ = \frac{AD}{BD} = \frac{a\sqrt{3}}{a} = \sqrt{3} $$
$$\sec 60^\circ = \frac{1}{\cos 60^\circ} = 2 $$
$$\mathrm{cosec} \: 60^\circ = \frac{1}{\sin 60^\circ} = \frac{2}{\sqrt{3}} $$
$$\cot 60^\circ = \frac{1}{\tan 60^\circ} = \frac{1}{\sqrt{3}}$$
✅ T-Ratios of 30° (from the same ΔADB):
- Base = AD = $a\sqrt{3}$
- Height = BD = a
- Hypotenuse = AB = 2a
$$\sin 30^\circ = \frac{BD}{AB} = \frac{a}{2a} = \frac{1}{2}$$
$$\cos 30^\circ = \frac{AD}{AB} = \frac{a\sqrt{3}}{2a} = \frac{\sqrt{3}}{2}$$
$$\tan 30^\circ = \frac{BD}{AD} = \frac{a}{a\sqrt{3}} = \frac{1}{\sqrt{3}}$$
$$\sec 30^\circ = \frac{1}{\cos 30^\circ} = \frac{2}{\sqrt{3}}$$
$$\mathrm{cosec} \: 30^\circ = \frac{1}{\sin 30^\circ} = 2 $$
$$\cot 30^\circ = \frac{1}{\tan 30^\circ} = \sqrt{3}$$
🧠 Axioms of Trigonometric Ratios
📍 For 0°:
We define:
- sin 0° = 0
- cos 0° = 1
- tan 0° = 0
- sec 0° = 1
❌ cosec 0° and cot 0° are undefined
📍 For 90°:
We define:
- sin 90° = 1
- cos 90° = 0
- cosec 90° = 1
- cot 90° = 0
❌ tan 90° and sec 90° are undefined
All Values of Trigonometric Ratios [Some Specific Angles]
Some of the common values of trigonometric ratios are listed in the following table:
| ∠A | 0° | 30° | 45° | 60° | 90° |
| sin A | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| cos A | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| tan A | 0 | 1/√3 | 1 | √3 | Not defined |
| cosecA | Not defined | 2 | √2 | 2/√3 | 1 |
| sec A | 1 | 2/√3 | √2 | 2 | Not defined |
| cot A | Not defined | √3 | 1 | 1/√3 | 0 |
MCQs on Trigonometric Ratios of 30°, 45°, and 60° for Class 10 Math
Multiple Choice Questions (MCQs) based on the geometric explanation of Trigonometric Ratios of 30°, 45°, and 60°, perfect for Class 10, Class 11, JEE, and NEET-level preparation
Q1. If in a triangle $\angle A = 30^\circ$, AB = 10 cm, and $\angle B = 90^\circ$, find the length of side AC.
A. 10 cm
B. 5√3 cm
C. 20 cm
D. 10√3 cm
✅ Correct Answer: D. $10\sqrt{3} cm$
🧠 Explanation:
In right triangle with $\angle A = 30^\circ$ :
$\cos 30^\circ = \frac{AB}{AC} \Rightarrow \frac{\sqrt{3}}{2} = \frac{10}{AC} \Rightarrow AC = \frac{10 \times 2}{\sqrt{3}} = \frac{20}{\sqrt{3}} = 10\sqrt{3}$
Q2. $\tan \theta = \frac{1}{\sqrt{3}}$, and $0^\circ < \theta < 90^\circ$, what is the value of $\cos \theta$ ?
A. $\frac{1}{\sqrt{2}}$
B. $\frac{1}{2}$
C. $\frac{\sqrt{3}}{2}$
D. 1
✅ Correct Answer: C. $\frac{\sqrt{3}}{2}$
🧠 Explanation:
If $\tan \theta = \frac{1}{\sqrt{3}} \Rightarrow \theta = 30^\circ \Rightarrow \cos 30^\circ = \frac{\sqrt{3}}{2}$
Q3. If $\sin \theta = \cos \theta$, then the value of $\theta$ is:
A. 30°
B. 45°
C. 60°
D. 90°
✅ Correct Answer: B. 45°
🧠 Explanation:
Only at 45°, $\sin \theta = \cos \theta = \frac{1}{\sqrt{2}}$
Q4. In a right triangle, the ratio of adjacent side to hypotenuse is $\frac{1}{2}$. The angle opposite to the perpendicular is:
A. 30°
B. 45°
C. 60°
D. 90°
✅ Correct Answer: C. 60°
🧠 Explanation:
$\cos \theta = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{1}{2} \Rightarrow \theta = 60^\circ$
Q5. If $\sin \theta = \frac{1}{2}$ and $0^\circ < \theta < 90^\circ$, then what is the value of $\tan \theta + \cot \theta$?
A. $\sqrt{3} + \frac{1}{\sqrt{3}}$
B. 2
C. $\frac{1}{\sqrt{3}} + \sqrt{3}$
D. 3
✅ Correct Answer: A. $\sqrt{3} + \frac{1}{\sqrt{3}}$
🧠 Explanation:
$\sin \theta = \frac{1}{2} \Rightarrow \theta = 30^\circ$
$\tan 30^\circ = \frac{1}{\sqrt{3}}, \quad \cot 30^\circ = \sqrt{3} \Rightarrow \text{Sum} = \frac{1}{\sqrt{3}} + \sqrt{3}$
Solved Examples on Trigonometric Ratios of 30°, 45°, and 60° for Class 10 Math
Find the value of: sin 30o cos 30o
Given sin 30o cos 30o
By substituting the values, we get
sin 30o cos 30o = ½ (√3/2) = √3/4
Find the value of: tan 30o tan 60o
Given tan 30o tan 60o
By substituting the values, we get
tan 30o tan 60o = 1/√3 (√3) = 1
Find the value of: cos2 60o + sin2 30o
Given cos2 60o + sin2 30o
By substituting the values, we get
cos2 60o + sin2 30o = (½)2 +(½)2 = ¼ + ¼ = ½
Find the value of: cosec2 60o – tan2 30o
Given cosec2 60o – tan2 30o
By substituting the values, we get
cosec2 60o – tan2 30o = (2/√3)2 – (1/√3)2
= 4/3 – 1/3 = 1
Find the value of: sin2 30o + cos2 30o + cot2 45o
Given sin2 30o + cos2 30o + cot2 45o
By substituting the values, we get
sin2 30o + cos2 30o + cot2 45o = (½)2 + (√3/2)2 + 12
= ¼ + ¾ + 1 = 2
Find the value of: cos2 60o + sec2 30o + tan2 45o
Given cos2 60o + sec2 30o + tan2 45o
By substituting the values, we get
cos2 60o + sec2 30o + tan2 45o = (½)2 + (2/√3)2 + 12
= ¼ + 4/3 + 1 = 31/12
Find the value of: tan2 30o + tan2 45o + tan2 60o
Given tan2 30o + tan2 45o + tan2 60o
By substituting the values, we get
tan2 30o + tan2 45o + tan2 60o = (1//√3)2 + 12 + (/√3)2
= 1/3 + 1 + 3 = 13/3 = 4 1/3
Find the value of: 3 sin2 30o + 2 tan2 60o – 5 cos2 45o.
Given 3 sin2 30o + 2 tan2 60o – 5 cos2 45o.
By substituting the values, we get
3 sin2 30o + 2 tan2 60o – 5 cos2 45o. = 3 (½)2 + 2 (√3)2 + 5 (1/√3)2
= ¾ + 6 – 5/2
= (3 + 24 – 10)/4 = 4 ¼
Prove that:
(i) sin 60o cos 30o + cos 60o. sin 30o = 1
(ii) cos 30o. cos 60o – sin 30o. sin 60o = 0
(iii) cosec2 45o – cot2 45o = 1
(iv) cos2 30o – sin2 30o = cos 60o.
(v) 3 cosec2 60o – 2 cot2 30o + sec2 45o = 0.
Solution :
(i) Given sin 60o cos 30o + cos 60o. sin 30o
LHS = sin 60o cos 30o + cos 60o. sin 30o
Now we have to prove that RHS = 1
= (√3/2) (√3/2) + ½ ½ = ¾ + ¼ = 1 = RHS
(ii) Given cos 30o. cos 60o – sin 30o. sin 60o = 0
LHS = cos 30o. cos 60o – sin 30o. sin 60o
= (√3/2) ½ – ½ (√3/2) = (√3/4) – (√3/4) = 0 = RHS
(iii) Given cosec2 45o – cot2 45o = 1
LHS = cosec2 45o – cot2 45o = 1
= (√2)2 – 12 = 2 – 1 = 1 = RHS
(iv) Given cos2 30o – sin2 30o = cos 60o.
LHS = cos2 30o – sin2 30o = cos 60o.
= (√3/2)2 – (½)2
= ¾ – ¼ = ½
= cos 60o = RHS
(v) Given 3 cosec2 60o – 2 cot2 30o + sec2 45o = 0.
LHS = 3 cosec2 60o – 2 cot2 30o + sec2 45o = 0.
= 3 (2/√3)2 – 2 (√3)2 + (√2)2
= 4 – 6 + 2 = 0 = RHS
Prove that:
(i) sin 60o = 2 sin 30o cos 30o.
(ii) 4 (sin4 30o + cos4 60o) – 3 (cos2 45o – sin2 90o) = 2
Solution:
(i) LHS = sin 60o = √3/2
RHS = 2 sin 30o cos 30o = 2 (√3/2) (½) = √3/2
Therefore LHS = RHS
(ii) LHS = 4 (sin4 30o + cos4 60o) – 3 (cos2 45o – sin2 90o)
Now by substituting the values we get
= 4[(½)4 + (½)4] – 3 [(1/√2)2 + 14]
= 4(1/16 + 1/16) – 3 (½ – 1)
= 8/16 + 3/2 = 2
LHS = RHS
Solve the given Problems, according to given statement
(i) If sin x = cos x and x is acute, state the value of x.
(ii) If sec A = cosec A and 0o ≤ A ≤ 90o, state the value of A.
(iii) If tan θ= cot θ and 0o ≤ θ ≤ 90o, state the value of θ.
(iv) If sin x = cos y; write the relation between x and y, if both the angles x and y are acute.
Solution:
(i) The angle, x is acute and hence we have, 0 < x
We know that
Cos2x + sin2 x = 1
Since cos x = sin x
Above equation will become
2 sin2 x = 1
Sin x = 1/√2
Therefore, x = 45o
(ii) sec A = cosec A
Cos A = sin A
Cos2 A = sin2 A
Cos2x + sin2 x = 1
Above equation will become
Cos2 A = 1 – cos2 A
2 cos2 A = 1
Cos A = 1/√2
A = 45o
(iii) tan θ = cot θ
tan θ = 1/tan θ
tan2 θ = 1
tan θ = 1
tan θ = tan 45o
θ = 45o
(iv) sin x = cos y = sin (90o – y)
If x and y are acute angles
x = 90o – y
which implies,
x + y = 90o
hence x and y are complementary angles.
State True or False the given statements
(i) If sin x = cos y, then x + y = 45o; write true of false.
(ii) sec θ. Cot θ = cosec θ; write true or false.
(iii) For any angle θ, state the value of: Sin2 θ + cos2 θ.
Solution:
(i) sin x = cos y = sin (π/2 – y)
If x and y acute angles,
x = (π/2 – y)
x + y = π/2
x + y = 45o is false
(ii) sec θ. Cot θ = 1/ cos θ. cos θ/ sin θ
= cosec θ
sec θ. Cot θ = cosec θ
is true.
(iii) Sin2 θ + cos2 θ = Sin2 θ + 1 – sin2 θ.
= 1
State for any acute angle θ whether:
(i) sin θ increases or decreases as θ increases:
(ii) cos θ increases or decreases as θ increases.
(iii) tan θ increases or decreases as θ decreases.
Solution:
(i) For acute angles, remember what sine means: opposite over hypotenuse. If we increase the angle, then the opposite side gets larger. That means “opposite/hypotenuse” gets larger or increases.
(ii)For acute angles, remember what cosine means: base over hypotenuse. If we increase the angle, then the hypotenuse side gets larger. That means “base/hypotenuse” gets smaller or decreases.
(iii)For acute angles, remember what tangent means: opposite over base. If we decrease the angle, then the opposite side gets smaller. That means “opposite /base” gets decreases.
If √3 = 1.732, find (correct to two decimal place) the value of each of the following: (i) sin 60o (ii) 2/ tan 30o
Solution:
(i) sin 60o = √3 /2
= 1.732/2 = 0.87
(ii) 2/ tan 30o = 2/ (1/√3)
= 2√3 = 2 (1.732) = 3.46
Given A = 60o and B = 30o, prove that:
(i) sin (A + B) = sin A cos B + cos A sin B
(ii) cos (A + B) = cos A cos B – sin A sin B
(iii) cos (A – B) = cos A cos B + sin A sin B
(iv) tan(A-B) = (tan A – tan B)/(1 + tan A tan B)
Solution:
(i) Given A = 60o and B = 30o
LHS = sin (A + B)
= sin (60o + 30o) = sin 90o = 1
RHS = sin A cos B + cos A sin B
= sin 60o cos 30o + cos 60o sin 30o
= √3/2 (√3/2) + ½ ½ = ¾ + ¼ = 1
LHS = RHS
(ii) LHS = cos (A + B)
= cos (60o + 30o) = cos 90o = 0
RHS = cos A cos B – sin A sin B
RHS = cos 60o cos 30o – sin 60o sin 30o
= ½ (√3/2) – (√3/2) ½ = √¾ – √3/4 = 0
LHS = RHS
(iii) LHS = cos (A – B)
= cos (60o – 30o) = cos 30o = √3/2
RHS = cos A cos B + sin A sin B
RHS = cos 60o cos 30o + sin 60o sin 30o
= ½ (√3/2) + (√3/2) ½ = √¾ + √3/4 = √3/2
LHS = RHS
(iv) LHS = tan (A – B)
= tan (60o – 30o) = tan 30o = 1/√3
RHS = (tan A – tan B)/(1 + tan A tan B)
(tan 60o – tan 30o)/(1 + tan 60o tan 30o)
= (√3 – 1/√3)/ 1 + √3 (1/√3)
= 2/ 2 √3 = 1/√3
Therefore, LHS = RHS
If tan (A+ B) =√3, tan (A-B) = 1/√3, then find A and B. [Given that 0° <A+B ≤ 90°; A>B ]
Solution:
Given that
tan (A+B) = √3.
We know that tan 60 = √3.
Thus, tan (A+B) = tan 60° = √3.
Hence A+B= 60° …(1)
Similarly, given that,
tan (A-B) = 1/√3.
We know that tan 30° = 1/√3.
Thus, tan (A-B) = tan 30° = 1/√3.
Hence, A-B = 30° …(2)
Now, adding the equations (1) and (2), we get
A+B+A-B = 60° + 30°
2A = 90°
A = 45°.
Now, substitute A = 45° in equation (1), we get
45° +B = 60°
B = 60°- 45°
B = 15°
Hence, A = 45 and B = 15°.
If sin θ + cos θ = √3, then prove that tan θ + cot θ = 1.
Solution:
Given,
sin θ + cos θ = √3
Squaring on both sides,
(sin θ + cos θ)2 = (√3)2
sin2θ + cos2θ + 2 sin θ cos θ = 3
Using the identity sin2A + cos2A = 1,
1 + 2 sin θ cos θ = 3
2 sin θ cos θ = 3 – 1
2 sin θ cos θ = 2
sin θ cos θ = 1
sin θ cos θ = sin2θ + cos2θ
⇒ (sin2θ + cos2θ)/(sin θ cos θ) = 1
⇒ [sin2θ/(sin θ cos θ)] + [cos2θ/(sin θ cos θ)] = 1
⇒ (sin θ/cos θ) + (cos θ/sin θ) = 1
⇒ tan θ + cot θ = 1
Hence proved.
💡 Do You Know?
- The values of trigonometric ratios are exact for 0°, 30°, 45°, 60°, and 90°.
- These ratios are frequently used in geometry, physics, astronomy, and engineering.
- The identities like sin²θ + cos²θ = 1 help derive all other formulas in trigonometry.
📘 Quick Summary Table
| Angle | sin | cos | tan | sec | cosec | cot |
|---|---|---|---|---|---|---|
| 0° | 0 | 1 | 0 | 1 | – | – |
| 30° | 1/2 | √3/2 | 1/√3 | 2/√3 | 2 | √3 |
| 45° | 1/√2 | 1/√2 | 1 | √2 | √2 | 1 |
| 60° | √3/2 | 1/2 | √3 | 2 | 2/√3 | 1/√3 |
| 90° | 1 | 0 | – | – | 1 | 0 |

