Two Point Form of Equation of Line Formula | Solved Examples | Practice Problems, FAQs, Important Questions

Class 11 Mathematics | Written by Neeraj Anand

Published by ANAND TECHNICAL PUBLISHERS

Introduction

The equation of a straight line can be determined using different forms based on given conditions. One of the most fundamental forms is the two-point form, which is used when the coordinates of two distinct points on the line are known.

Understanding the Two-Point Form

In coordinate geometry, a straight line is uniquely determined if two of its points are given. The two-point form provides a mathematical relationship between these two points, making it a crucial concept for solving problems related to straight lines in Class 11 Mathematics and competitive exams like JEE Mains & Advanced.

Concept Behind the Two-Point Form

When a line passes through two points, it means that every point on the line follows a specific relationship based on the coordinates of the given points. This form helps in deriving the equation of the line by considering the variation in the x-coordinates and y-coordinates of these two points.

Derivation of Two Point Form of the Equation of a Line

Let P₁ (x₁, y₁) and P₂ (x₂, y₂) be the two given points on the line L.

Let P(x, y) be a general point on the line L.

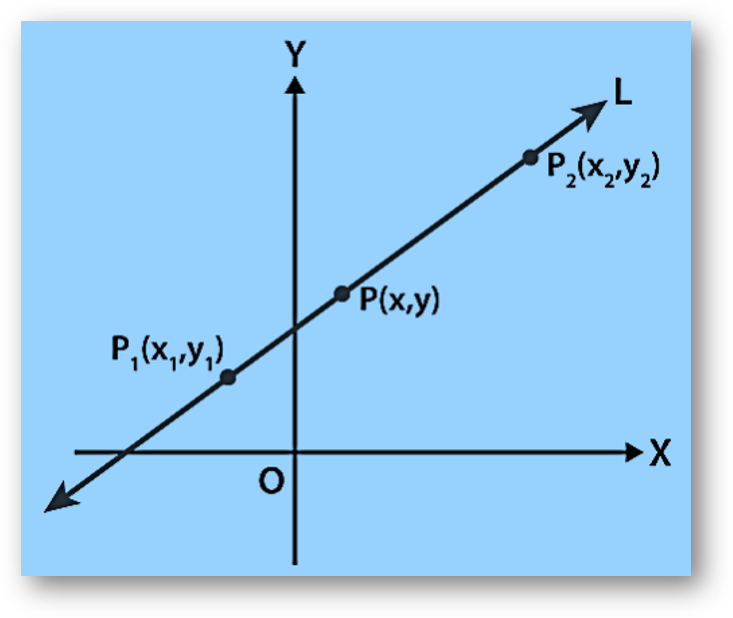
From the above figure, we can say that the three points P₁, P₂ and P are collinear.

That means,

Slope of P₁P = Slope of P₁P₂

The ratio of difference of y-coordinates of P and P1 to the difference of x-coordinates of these points = The ratio of difference of y-coordinates of P1 and P2 to the difference of x-coordinates of these points

\(\begin{array}{l}\large \frac{y-y_{1}}{x-x_{1}}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\end{array} \)

Or

\(\begin{array}{l}\large {y-y_{1}}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1})\end{array} \)

Thus, equation of the line passing through the points (x₁, y₁) and (x₂, y₂) is given by

\(\begin{array}{l}\large {y-y_{1}}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1})\end{array} \)

This is the equation of a line in two-point form.

Two Point Form Solved Examples

Example 1: Find the equation of a line passing through the points (-2, 3) and (3, 5).

Solution:

Let the given points be:

(x₁, y₁) = (-2, 3)

(x₂, y₂) = (3, 5)

The equation of a straight line passing through the points (x₁, y₁) and (x₂, y₂) is given as:

\(\begin{array}{l}{y-y_{1}}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1})\end{array} \)

Substituting the values, we get;

\(\begin{array}{l}{y-3}=\frac{5 – 3}{3-(-2)}[x -(2)]\end{array} \)

y – 3 = (2/5) (x + 2)

5(y – 3) = 2(x + 2)

5y – 15 = 2x + 4

2x + 4 – 5y + 15 = 0

2x – 5y + 19 = 0

Hence, this is the required equation of a line passing through the given points.

Example 2: What is the equation of a straight line passing through the points (2, 0) and (0, 2)?

Solution:

Let the given points be:

(x₁, y₁) = (2, 0)

(x₂, y₂) = (0, 2)

The equation of a straight line passing through the points (x₁, y₁) and (x₂, y₂) is given as:

\(\begin{array}{l}{y-y_{1}}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1})\end{array} \)

Substituting the values, we get;

\(\begin{array}{l}{y-0}=\frac{2 – 0}{0 – 2}(x – 2)\end{array} \)

y = (-2/2) (x – 2)

y = -1(x – 2)

y = -x + 2

x + y – 2 = 0

Therefore, the equation of a line passing through the given points (2, 0) and (0, 2) is x + y – 2 = 0.

Example 3: Find the equation of the line passing through the points A(-2, 3) and B(3, 5).

Solution:

Given points are:

• A = (-2, 3)
• B = (3, 5)

Using the formula, we get:

⇒ (y-3) = {(5 – 3)/(3 -(-2))}.(x + 2)

⇒ (y – 3) = 2/5.(x+2)

⇒ 5y – 15 = 2x + 4

⇒ 5y = 2x + 19

Thus, the equation of the line is 5y = 2x + 19

Example 4: Find the equation of the line passing through the points A(0,3) and B(3,0).

Solution:

Given points are:

• A = (0, 3)
• B = (3, 0)

Using the formula, we get:

⇒(y – 0) = {(3 – 0)/(0 – (-3)}(x-3)

⇒ y = {3/3}(x-3)

⇒ 3y = 3x-9

Thus, equation of the line is 3y = 3x – 9

Example 5: Find the equation of a straight line whose x-intercept is ‘a’ and y-intercept is ‘b’ ?

Solution :

Given points are:

• A = (a, 0)
• B = (0, b)

Using the formula, we get:

⇒ (y-0) = (b-0) (x-a) / (0-a)

⇒ y = b(x-a) / (-a)

⇒ -ay = bx – ba

⇒ ay + bx = ab

Thus, the equation of the line is ay + bx = ab

Example 6: Write the equation of the line through the points (3, –3) and (1, 5).

Solution:

Given points are:

• A = (3, -3)
• B = (1, 5)

Using the formula, we get:

⇒ (y + 3) = (5 + 3) (x – 3) / (1-3)

⇒ (y + 3) = -4(x – 3)

⇒ y+3 = -4x+12

⇒ 4x + y = 9

Thus, the equation of the line is 4x + y = 9

Example 7: Derive the y-intercept of the line with the coordinates given by A(3,-2) & B(1,-3) passing through it and also find the slope m of the line.

Solution:

Given points are:

• A = (3, -2)
• B = (1, 5)

Using the formula, we get:

⇒ (y + 2) = (5 + 2) (x – 3) / (1-3)

⇒ (-2)(y + 2) = 7(x – 3)

⇒ -2y – 4 = 7x – 21

⇒ 7x + 2y = 17

Thus, the equation of the line is 7x + y = 9

To find slope compare the given equation with,

y = mx + c

Given equation:

7x + y = 9

⇒ y = -7x + 9

Hence, m = -7

Thus, the slope of the line is -7

Practice Questions on Two Point Form

Q1: What is the slope of a line passing through the points (5, -4) and (-3, 6)?

Q2: What is the slope of a line passing through the points (5, 0) and (0, 5)?

Q3: Derive the y-intercept of the line with the coordinates given by A(3, -2) and B(-1, 3) passing through it and also find the slope m of the line.

Q4: What is the equation of a vertical line passing through the point A(4, -7).

Q5: What is the slope of a line passing through the points (10, 5) and (6, 12)?

Q6: What is the slope of a line passing through the points (3, -9) and (-3, -7)?

Q7: Write the equation of the line through the points (3, –3) and (1, 5).

Q8 : Find the equation of a straight line passing through the points (–4, 2) and (6, -7).

Q9: What is the equation of the line joining the points (6, 3) and (-5, 2)?

Two Point Form – FAQs

What is the two point form?

Two-point form of a line is the equation of a line when two points on a line are given, the two-point form formula is Y − y₁ = (y₂ − y₁)/(x₂ − x₁)(X − x₁). Where the two points are, (x₁, y₁) and (x₂, y₂)

How do you determine whether a point lies on a line?

Every point on a line satisfies its line equation. For example, to see whether (3, 6) lies on a line y=2x, we substitute x=3 & y=6 in the given equn. Then we get – 6=2(3) or 6=6. The equation is satisfied and hence the point (3, 6) lies on the line y=2x.

What is the point slope form?

The equation of line in point slope form is given by : (y-y₁) = m(x-x₂) .

What is the equation of x-axis?

The equation of x-axis is : y=0

What is the equation of y-axis?

The equation of y-axis is : x=0

Give an example of a two point form?

Point A with coordinates (2, 3) and Point B with coordinates (4, 7). To find the equation of the line that goes through these points, we substitute the coordinates into the two-point formula:

• x₁ = 2, y₁ ​= 3
• x₂ = 4, y₂ = 7

Substituting these values into the equation gives us:

y−3=(7−3)/(4−2)

Applications of the Two-Point Form

1. Finding the Equation of a Line – If two points are given, this form helps in determining the general equation of the line.
2. Checking Collinearity – If a third point satisfies the equation derived using two points, it confirms that all three points lie on the same line.
3. Slope Calculation – The two-point form is useful in calculating the slope of a line when only two points are known.
4. Intersection of Lines – Used to determine whether two lines intersect by solving their equations simultaneously.
5. Physics and Engineering Applications – Straight-line equations are frequently used in mechanics, kinematics, and electrical circuits to model relationships.

Key Points to Remember

• This form is particularly useful when the slope is not directly given but can be calculated from two points.
• The equation derived from this form can be converted into other forms like the slope-intercept form, standard form, and intercept form based on problem requirements.
• It provides a straightforward way to establish the equation of a straight line in coordinate geometry.

Conclusion

The two-point form of the equation of a line is an essential topic in Class 11 Mathematics, providing a foundational tool for solving numerous geometry problems. It is widely used in board exams and entrance tests like JEE Mains & Advanced, making it important for students to master.

📥 Download PDF

Students preparing for CBSE Board & JEE Mains/Advanced can download the full PDF from ANAND CLASSES for detailed explanations and additional solved examples. 🚀